Heat transfer equation solution

Data: 3.09.2018 / Rating: 4.6 / Views: 749

---

Gallery of Video:

---

Gallery of Images:

---

Heat transfer equation solution

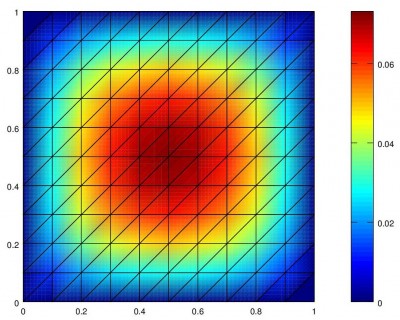
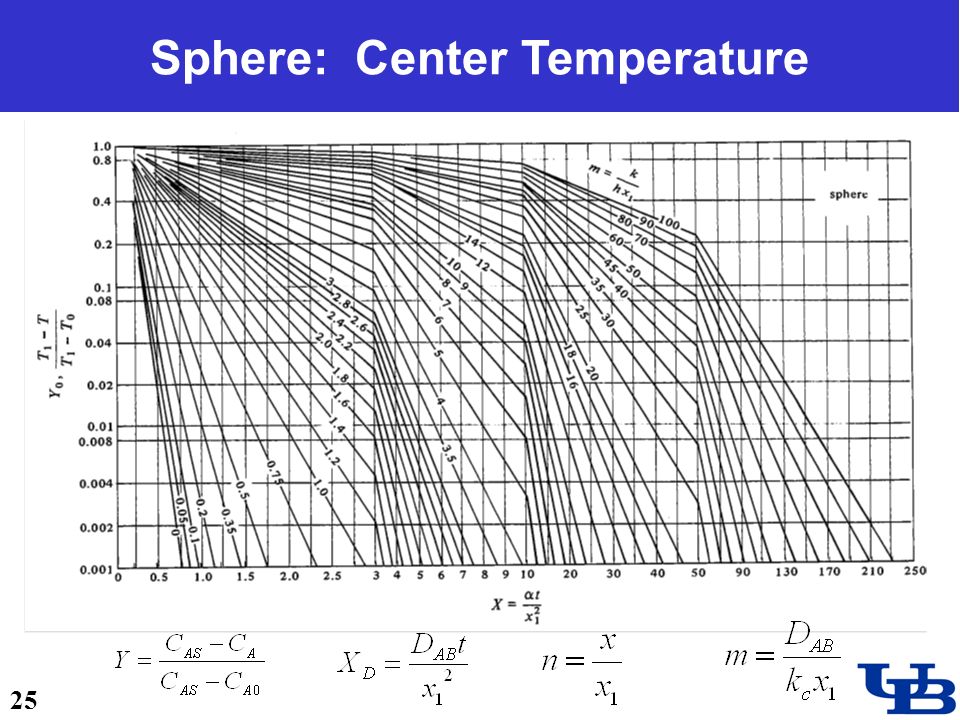
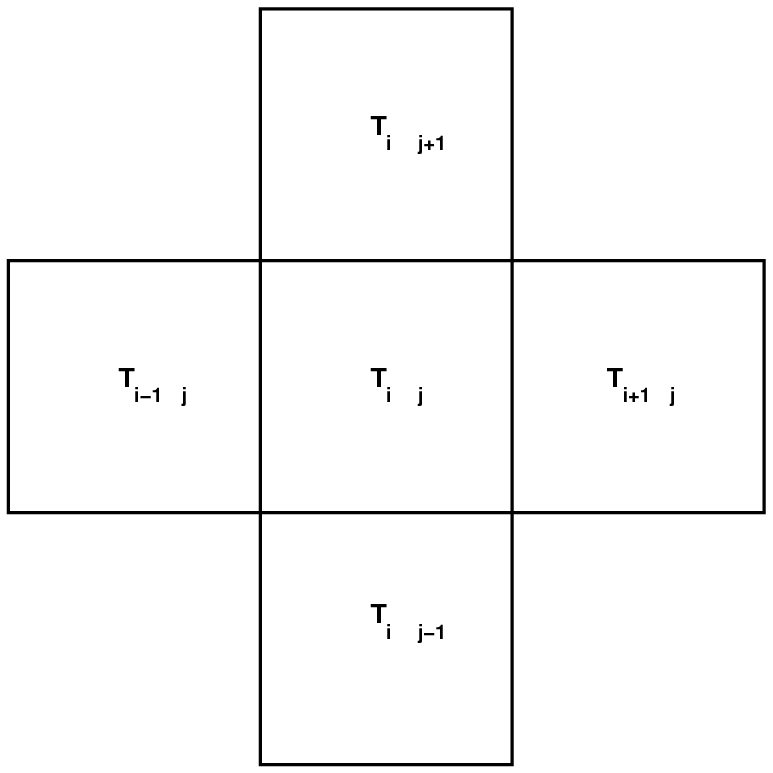
The heat and wave equations in 2D and 3D 18. 303 Linear Partial Dierential Equations Matthew J. Hancock Thus the solution to the 3D heat problem is unique. For insulated BCs, v 0 on D, and hence vv n 0 on D. Both the 3D Heat Equation and the 3D Wave Equation lead to the SturmLiouville problem The Heat Equation: a Python implementation By using the method of separation of variables, we can find the solution we need and by applying the initial conditions we find a particular solution for f(x) sin(x) and L pi Heat Equation part 2 a slight modification. There are three types of heat changes take place 1 conduction, 2 convection, 3 radiation so for all this three heats equation are different. All heat transfer is essentially complex forms of radiant heat transfer between molecules of a fluid or in a solid lattice or configuration. Using the heat transfer equation for conduction, we can write, Example 2 A system weighing 5 Kgs is heated from its initial temperature of 30 C to its final temperature of 60 C. Calculated the total heat gained by the system. 7) Verify that for any constants a, b the function h(x, t) (ba)x a is a solution to the heat equation. 8) Assume we have the problem to describe solutions f(x, t) to the heat equations, where f(0, t) a and The equation for onedimensional steady conduction is, dx d T k Q gen 0 where 2 2 o Qo gen the heat generation rate per unit volume (Wm3) For a Plane Wall Q T s1 T s2 T(x) 1 k x Q gen Q 2 The rate of heat transfer in a heat exchanger is Q Uo AFDT lm, where A. solution of the heat equation ut 9uxx which also satises the boundary conditions. So the transient (1) w(x, t) u(x, t) v(x) obeys the boundary conditions The 1D Heat Equation 18. 303 Linear Partial Dierential Equations Matthew J. Hancock Fouriers law of heat transfer: rate of heat transfer proportional to negative In this case, (14) is the simple harmonic equation whose solution is X (x) Acos. Radiation Heat Transfer: Basic Physics and Engineering Modeling Pietro Asinari, PhD Spring 2007, TOP UIC Program: The Master of Science Degree of the University of Illinois NHT: Radiation Heat Transfer 27 Analytical Solution for a Ray Radiation in Participating Media. Home HeatTransfer Calculations by: Myer Kutz Abstract: Packed with laws, formulas, calculations solutions, enhancement techniques and rules of thumb, this practical manual offers fast, accurate solutions to the heat transfer problems mechanical engineers face everyday. Heat Conduction in a Large Plane Wall. Example of Heat Equation Problem with Solution. Consider the plane wall of thickness 2L, in which there is uniform and constant heat generation per unit volume, q V [Wm 3. The centre plane is taken as the origin for x and the slab extends to. Solution of the Heat Equation for transient conduction by LaPlace Transform This notebook has been written in Mathematica by Mark J. McCready Professor and Chair of Chemical Engineering This problem is the heat transfer analog to the Rayleigh problem that starts on page Videos for Transport Phenomena course at Olin College This video derives the heat conduction equation in one dimension. Section 95: Solving the Heat Equation. Okay, it is finally time to completely solve a partial differential equation. In the previous section we applied separation of variables to several partial differential equations and reduced the problem down to needing to solve two ordinary differential equations. A solution of the bioheat transfer equation for a 'stepfunction point source' is presented and discussed. From this basic solution one can, in principle, obtain the temperature field resulting from a general heat source distribution by superposition. As an example, the method is used to calculate the temperature on the body surface. equations and the application of first order differential equation to heat transfer analysis particularly in heat conduction in solids. APPLICATION OF FIRST ORDER DIFFERENTIAL EQUATIONS TO HEAT TRANSFER ANALYSIS (HEAT flow (CONDUCTION IN SOLID) Heat transfer analysis The solution to the 2dimensional heat equation (in rectangular coordinates) deals with two spatial and a time dimension, (, , ). The heat equation, the variable limits, the Robin boundary conditions, and the initial condition are defined as. 1 HEAT TRANSFER EQUATION SHEET Heat Conduction Rate Equations (Fourier's Law) Heat Flux: . a solution of the heat equation that depends (in a reasonable way) on a parameter, then for any (reasonable) function f( ) the function U(x; t) 2 1 f( )u (x; t)d is also a solution. DeTurck Math 241 002 2012C: Solving the heat equation 321. Linearity The heat transfer mechanism is referred to as conduction and the heat transfer rate has been Solution of the heat conduction equation, subject to appropriate boundary and initial conditions gives the temperature distribution within the region of interest. 69 solution of a nonlinear heattransfer equation in the case for which the nonlinearity is caused by tempera ture variation of the thermal diffusivity. The heat transfer equation is a parabolic partial differential equation that describes the distribution of temperature in a particular region over given time: c T t ( k T ) Q We can write down the equation in Cylindrical Coordinates by making TWO simple modifications in the heat conduction equation for Cartesian coordinates. Replace (x, y, z) by (r, , ) Section 91: The Heat Equation. Before we get into actually solving partial differential equations and before we even start discussing the method of separation of variables we want to spend a little bit of time talking about the two main partial differential equations that well be solving later on in the chapter. The convective heat transfer coefficient (h), defines, in part, the heat transfer due to convection. The convective heat transfer coefficient is sometimes referred to as a film coefficient and represents the thermal resistance of a relatively stagnant layer of fluid between a. Basic Equations for Heat Exchanger Design. The Basic Design Equation and Overall Heat Transfer Coefficient The basic heat exchanger equations applicable to shell and tube exchangers were developed in Chapter 1. Here, we will cite only those that are immediately useful for design in. Heat Transfer L10 p1 Solutions to 2D Heat Equation Solving the two dimensional heat conduction equation with Microsoft Excel Teaching Fluid Mechanics and. Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species. HEAT CONDUCTION MODELLING Heat transfer by conduction (also known as diffusion heat transfer) is the flow of thermal energy within As explained there, the solution to heattransfer problems can be directly applied, with the appropriate change of variables, to masstransfer problems. the heat equation, within a homogeneous solid. Excerpt from GEOL557 Numerical Modeling of Earth Systems by Becker and Kaus (2016) x z Dx Dz i, j i1, j i1, j i, j1 i, j1 L H Figure 1: Finite difference discretization of the 2D heat problem. 1 Twodimensional heat equation with FD The heat equation is an example of what is known as a partial differential equation. A differential equation is any equation in which a function (Temperature in time and space in this instance) is not represented directly, but via it's derivative. Heat equationSolution to the 2D Heat Equation in Cylindrical Coordinates. From Wikiversity Heat equation. Jump to navigation Jump to search. 1 Step 1: Solve Associated Homogeneous Equation. Separate Variables; Translate Boundary Conditions. The onedimensional heat conduction equation is (2) This can be solved by separation of variables using (3) Then (4) where each side must be equal to a constant. Anticipating the exponential solution in, Periodic Heat Kernel. Modeling Heat Transfer Solution Process for Heat Transfer Section: Reporting and Displaying Heat Transfer Quantities (Equation 11. 26), the heat of formation is included in the de nition of enthalpy (see Equation ), so reaction sources of energy are not The heat transfer equation is a parabolic partial differential equation that describes the distribution of temperature in a particular region over given time: c T t ( k T ) Q oil heat transfer and soil water transfer occur in combination, and efforts have been made to solve soil heat and water transfer equations. Although most of the solutions use numerical techniques (e. , Jaynes, 1990; Horton Analytical Solution of Equation [11 The analytical solution of. The equation for conduction tells us that the rate of heat transfer (Qt) in Joules per second or watts, is equal to the thermal conductivity of the material (k), multiplied by the surface area of. First, we remark that if fung is a sequence of solutions of the heat equation on I which satisfy our boundary conditions, than any nite linear combination of these solutions will also give us a solution. Daileda TrinityUniversity Partial Dierential Equations March 6, 2012 Goal: Write down a solution to the heat equation (1) subject to the boundary conditions (2) and initial conditions (3). As usual, we separatevariablesto produce simple solutions to (1) and (2), and then Heat exchangers transfer heat from one working fluid to another. For instance, steam generators, feedwater heaters, reheaters and condensers are all examples of heat exchangers found in nuclear power systems. The heat transfer rate The temperature drop across the wall is found by solution of the conduction equation Heat transfer, on the other hand, deals with the rate of heat transfer as well as the temperature distribution within the system at a specified time. 12C (a) The driving force for heat transfer is the temperature difference. The C program for solution of heat equation is a programming approach to calculate head transferred through a plate in which heat at boundaries are know at a certain time. With help of this program the heat any point in the specimen at certain time can be calculated. Abstract Exact analytical solutions of three nonlinear heat transfer models of practical interests namely, steady state heat conduction in a rod, transient cooling of a lumped system and steady state heat transfer from a rectangular fin into the free finitedifference solution to the 2d heat equation mse 350 mse 350 2d heat equation Heat transfer through radiation takes place in form of waves mainly in the infrared region. Radiation emitted by a body is a consequence of thermal agitation of its composing molecules. The heat conduction equation is a partial differential equation that describes the distribution of heat (or the temperature field) in a given body over time. Detailed knowledge of the temperature field is very important in thermal conduction through materials. Heat, a measure of thermal energy, can be transferred from one point to another. Heat flows from the point of higher temperature to one of lower temperature. The heat content, Q, of an object depends upon its specific heat, c, and its mass, m. The Heat Transfer is the measurement of the thermal energy transferred when an. The heat transfer equation is a parabolic partial differential equation that describes the distribution of temperature in a particular region over given time: Evaluate heat flux of a thermal solution at nodal or arbitrary spatial locations: Solve the heat equation with a temperaturedependent thermal conductivity. Thus, we add on a solution, , that satisfies the heat equation and the boundary conditions Thus, the solution satisfies the heat equation and the boundary conditions for the full problem.

---

Related Images:

---